| Abbrev | Film | Clip Start | Clip Stop | Duration |
|---|---|---|---|---|
| PursuitHappyness | The Pursuit of Happyness (2006) | 00:24:21.700 | 00:28:18.700 | 237 |
The Pursuit of Happyness
Film Information
The Pursuit of Happyness is a 2006 American biographical drama film directed by Gabriele Muccino and starring Will Smith as Chris Gardner, a homeless salesman. Smith’s son Jaden Smith co-stars, making his film debut as Gardner’s son, Christopher Jr. The screenplay by Steven Conrad is based on the best-selling 2006 memoir of the same name written by Gardner with Quincy Troupe. It is based on Gardner’s nearly one-year struggle being homeless. The unusual spelling of the film’s title comes from a mural that Gardner sees on the wall outside the daycare facility his son attended. The movie is set in San Francisco in 1981.
All information in this section came from Wikipedia.
Clip Information
Chris is hoping to get a job as a stockbroker. He shares a cab with Mr. Twistle, a lead manager and partner for the firm he is hoping to work at.
| Characteristic | Value |
|---|---|
| Format | MPEG-4 |
| File Size | 73.2 MiB |
| Duration | 237.029 |
| Frame Rate | 23.976 |
| Video Width | 1920 |
| Video Height | 800 |
| Video BitRate | 2.5 MB/s |
| Audio Channels | 2 |
| Audio SamplingRate | 48000 |
| Audio BitRate | 132.3 kB/s |
Subtitles
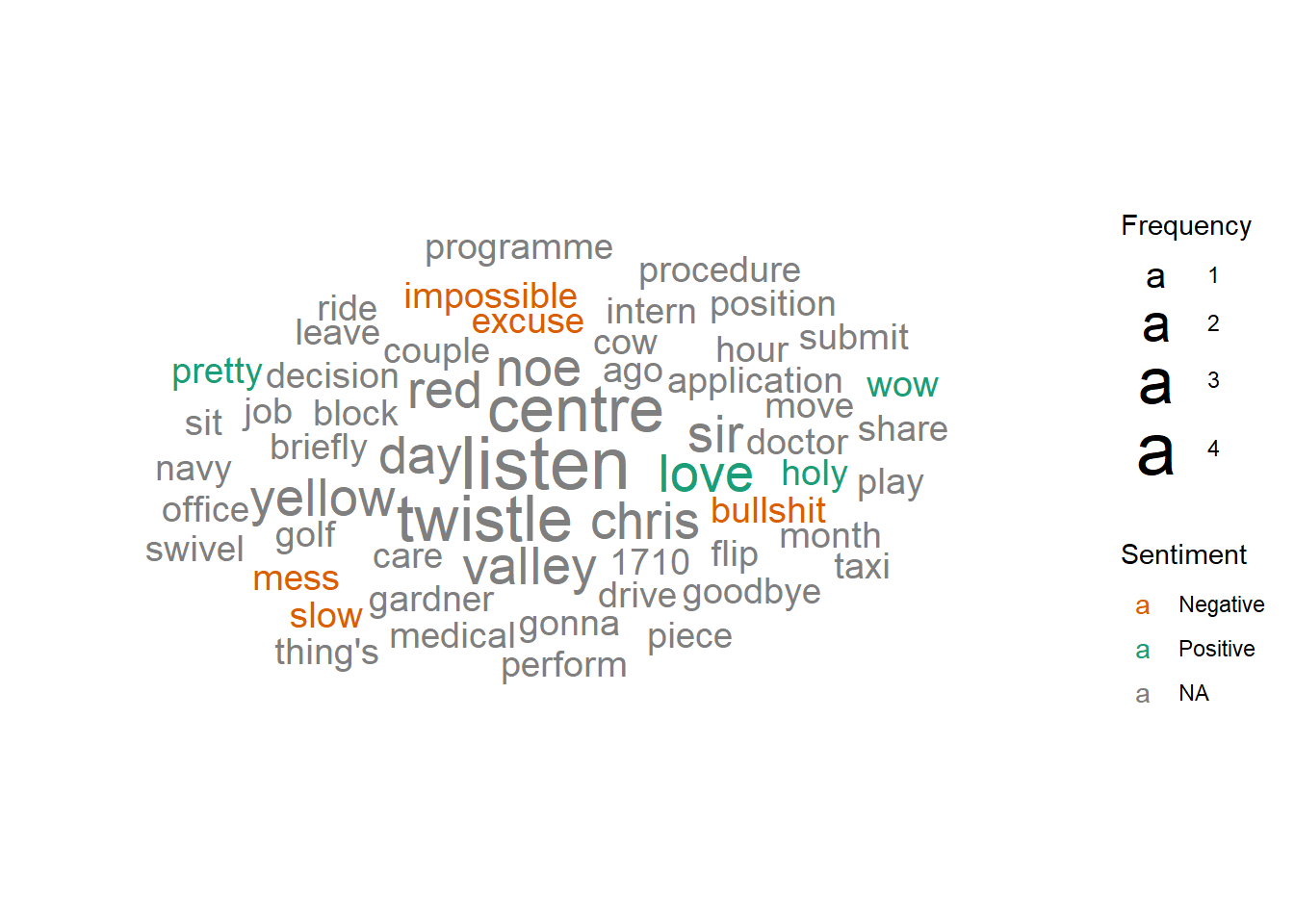
The following wordcloud shows the words used in this clip, scaled by number of occurrences and colored by sentiment (orange = negative, green = positive, grey = neutral or unsure). Note that the words have been stemmed and lemmatized and stopwords have been removed.
The table below shows all subtitles in this clip with the start and stop time of each subtitle’s appearance in seconds.
| Start | End | Subtitle |
|---|---|---|
| 2.163 | 4.374 | - Taxi! - Mr. Twistle. |
| 4.583 | 7.252 | - Yeah, hi. - Hi. Chris Gardner. |
| 7.502 | 9.296 | Yeah, hi. Listen. What can I do for you? |
| 9.504 | 12.549 | I submitted an application for the intern programme about a month ago... |
| 12.757 | 15.010 | ...and I would just love to sit with you briefly... |
| 15.260 | 17.178 | Listen, I'm going to Noe Valley, Chris. |
| 17.429 | 20.682 | - Take care of yourself. - Mr. Twistle. |
| 20.932 | 23.226 | Actually, I'm on my way to Noe Valley also. |
| 23.435 | 25.186 | How about we share a ride? |
| 26.688 | 28.857 | - All right, get in. - All right. |
| 34.946 | 37.699 | So when I was in the Navy, I worked for a doctor... |
| 37.949 | 40.744 | ...who loved to play golf, hours every day... |
| 40.952 | 45.582 | ...and I would actually perform medical procedures... |
| 45.790 | 47.334 | ...when he'd leave me in the office. |
| 47.542 | 52.797 | So I'm used to being in a position where I have to make decisions and... |
| 54.299 | 57.093 | Mr. Twistle, listen. This is a very important... |
| 57.302 | 59.512 | I'm sorry. I'm sorry. This thing's impossible. |
| 61.640 | 63.725 | - I can do it. - No, you can't. No one can. |
| 63.975 | 66.645 | - That's bullshit. - No, I'm pretty sure I can do it. |
| 67.062 | 70.232 | - No, you can't. - Let me see it. |
| 70.815 | 72.025 | Give it here. |
| 74.986 | 79.282 | Oh, yeah. Oh, wow, you really messed it up. |
| 79.491 | 81.034 | Sorry. |
| 81.576 | 87.541 | It looks like it works around a swivel, so the centre pieces never move. |
| 87.749 | 90.835 | So if it's yellow in the centre, that's the yellow side. |
| 91.086 | 93.547 | If it's red in the centre, that's the red side. |
| 93.755 | 97.384 | - Okay. - So... You can slow down. |
| 97.592 | 100.637 | Listen, we can drive around all day. I don't believe you can do this. |
| 100.845 | 102.556 | - Yeah, I can. - No, you can't. |
| 102.764 | 103.932 | - Yes, I can. - No, you can't. |
| 104.182 | 106.059 | I'm telling you, no one can. |
| 108.019 | 110.230 | See? That's all I ever do. |
| 123.118 | 125.412 | You almost have this side. |
| 126.037 | 127.497 | Holy cow. |
| 137.716 | 141.511 | - You almost had that one. - I'm gonna get it. |
| 149.060 | 150.812 | Look at that. |
| 174.085 | 175.295 | You're almost there. |
| 199.027 | 202.739 | - 1710. - This is me. |
| 204.866 | 206.243 | Good job. |
| 208.119 | 211.206 | - Goodbye. - Yeah. I'll see you soon. |
| 213.625 | 215.335 | Where are you going, sir? |
| 215.544 | 218.547 | Excuse me, sir. Where are you going, please? |
| 221.883 | 223.593 | Two... A couple of blocks. |
| 223.802 | 227.222 | - Just flip around. - Okay. |
Holistic Ratings
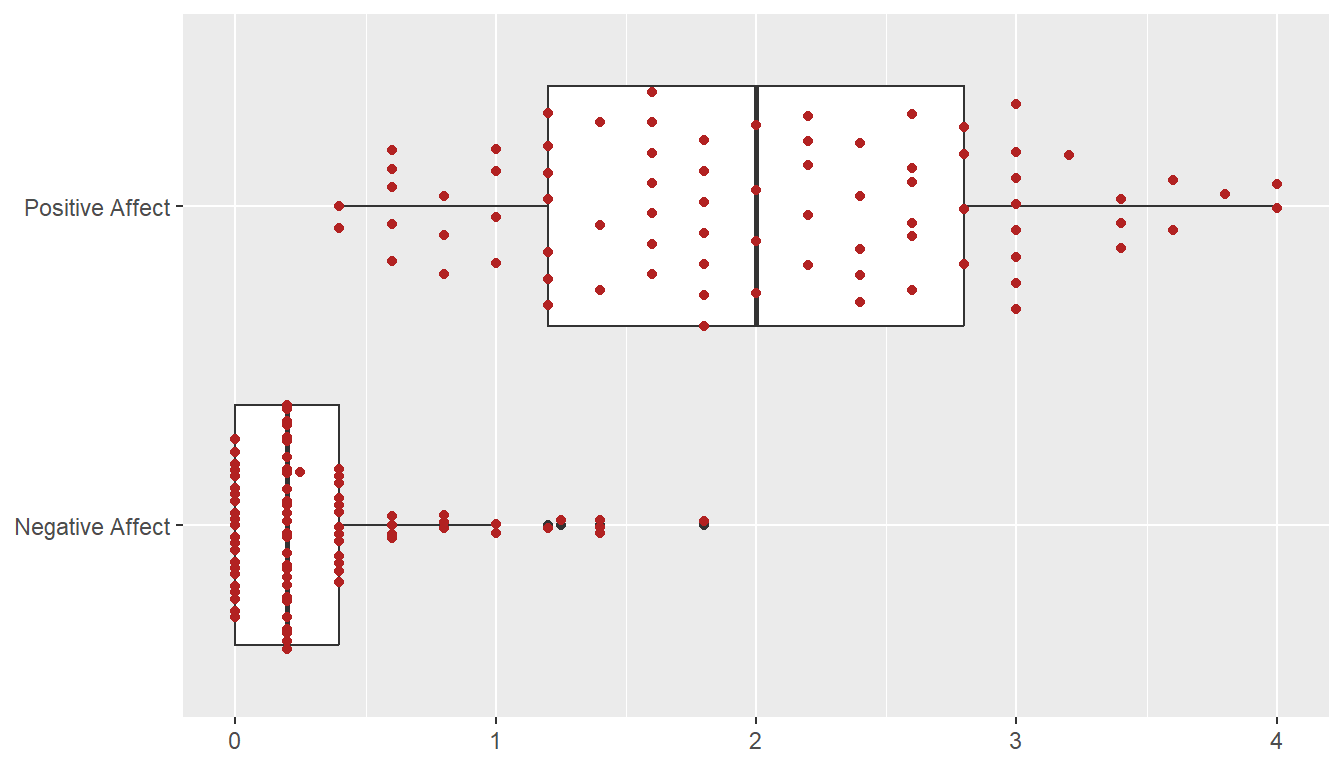
A total of 79 participants watched this film clip and then provided holistic ratings on how the entire clip made them feel. These holistic ratings were completed using five Positive Affect items (i.e., alert, determined, enthusiastic, excited, inspired) and five Negative Affect items (i.e., afraid, distressed, nervous, scared, upset), each rated on an ordinal scale from 0 to 4. The plot below shows the
Dynamic Ratings
A total of 79 participants watched this film clip and used the CARMA software to provide continuous (i.e., second-by-second) ratings of how it made them feel. These continuous ratings were made on a single emotional valence scale ranging from -4 (very negative) to 4 (very positive).
Time Series
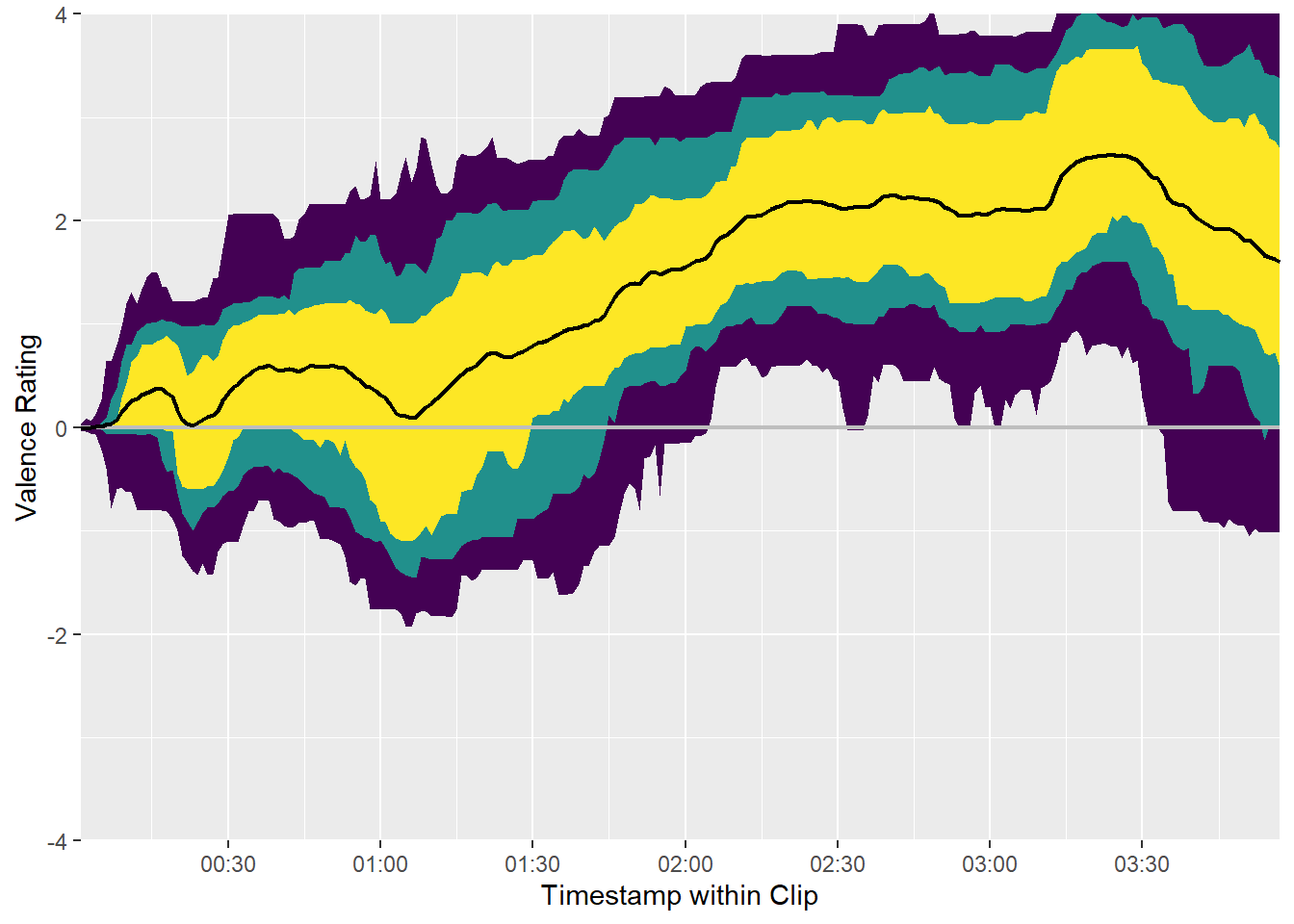
We can plot the distribution of all valence ratings per second of the film clip to get a sense of how its emotional tone changes over time. The solid black line represents the mean of all ratings and the yellow, green, and purple ribbons represent the central 50%, 70%, and 90% of the ratings, respectively.
Inter-Rater Reliability
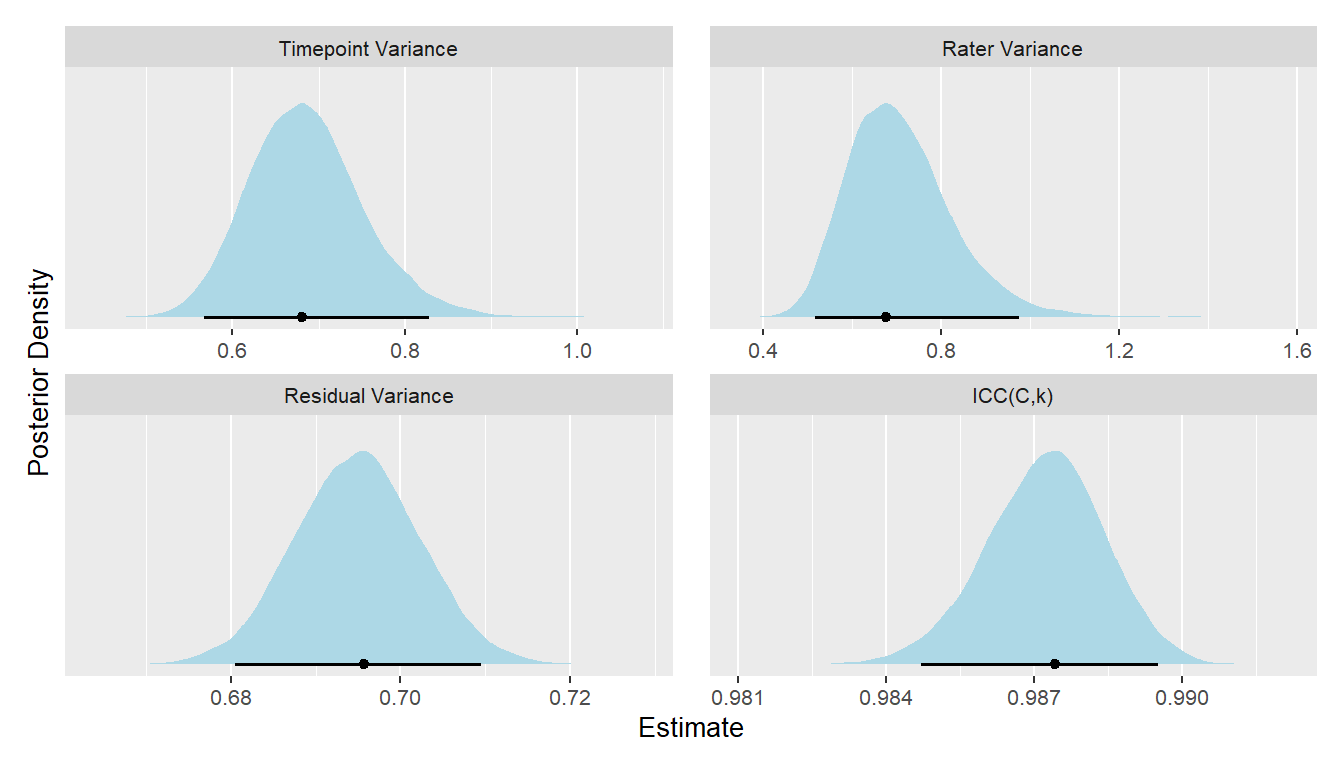
A Bayesian generalizability study was used to decompose the variance in ratings of this video clip into the following components: timepoint variance (in average ratings of each second, across raters), rater variance (in average ratings from each rater, across seconds), and residual variance (including second-by-rater interactions and measurement error). The lower and upper columns in the table below represent the boundaries of the 95% equal-tail credible interval. Note that we dropped the first 10 seconds of each clip (as rater “warmup” time).
| Component | Term | Estimate | Lower | Upper | Percent |
|---|---|---|---|---|---|
| Rater | Variance | 0.675 | 0.516 | 0.975 | 0.329 |
| Timepoint | Variance | 0.681 | 0.566 | 0.828 | 0.332 |
| Residual | Variance | 0.696 | 0.680 | 0.710 | 0.339 |
From these variance components, we can estimate inter-rater reliability of the ratings. There are many formulations of the two-way intraclass correlation (ICC), but the most relevant to our purposes here is the balanced average-measures consistency formulation or ICC(C,k).
| Term | Estimate | Lower | Upper | Raters | Error |
|---|---|---|---|---|---|
| ICC(C,k) | 0.987 | 0.985 | 0.99 | 79 | Relative |
Below, we can also visualize the posterior distributions of each of these parameters. Values with higher posterior density are more probable.
